Appearance
题目描述
https://leetcode.cn/problems/minimum-cost-to-reach-destination-in-time
一个国家有 n 个城市,城市编号为 0 到 n - 1 ,题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示,其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路,耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路,但是不会有道路两头连接着同一座城市。
每次经过一个城市时,你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示,其中 passingFees[j] 是你经过城市 j 需要支付的费用。
一开始,你在城市 0 ,你想要在 maxTime 分钟以内 (包含 maxTime 分钟)到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 (包括 起点和终点城市的通行费)。
给你 maxTime,edges 和 passingFees ,请你返回完成旅行的 最小费用 ,如果无法在 maxTime 分钟以内完成旅行,请你返回 -1 。
示例 1: 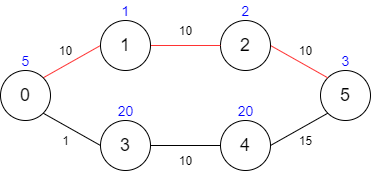
输入:maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:11
解释:最优路径为 0 -> 1 -> 2 -> 5 ,总共需要耗费 30 分钟,需要支付 11 的通行费。
示例 2: 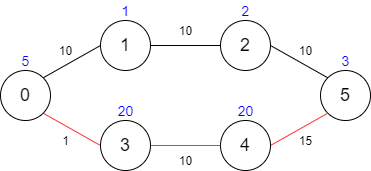
输入:maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:48
解释:最优路径为 0 -> 3 -> 4 -> 5 ,总共需要耗费 26 分钟,需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ,因为这条路径耗费的时间太长。
示例 3:
输入:maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出:-1
解释:无法在 25 分钟以内从城市 0 到达城市 5 。
提示:
- 1 <= maxTime <= 1000
- n == passingFees.length
- 2 <= n <= 1000
- n - 1 <= edges.length <= 1000
- 0 <= xi, yi <= n - 1
- 1 <= timei <= 1000
- 1 <= passingFees[j] <= 1000
- 图中两个节点之间可能有多条路径。
- 图中不含有自环。
思路 : 回溯法(会超时)
从开始的路线,深度优先搜索,满足条件 start == end 判断时间是否在里面。
csharp
public class Solution {
bool[] used;
int minFee = int.MaxValue;
private void dfs(int maxTime, int[][] edges, int[] passingFees, int start, int end, int fee, int time){
if(start >= end){
fee += passingFees[start];
if(time <= maxTime){
minFee = Math.Min(fee,minFee);
}
return;
}
for(int i=0; i<edges.Length; i++){
if(edges[i][0] == start && !used[start]){
used[start] = true;
dfs(maxTime,edges,passingFees, edges[i][1], end, fee + passingFees[start] , time + edges[i][2] );
used[start] = false;
}
}
}
public int MinCost(int maxTime, int[][] edges, int[] passingFees) {
int n = passingFees.Length;
used = new bool[n];
dfs(maxTime, edges, passingFees, 0, n - 1, 0, 0);
return minFee == int.MaxValue ? -1 : minFee;
}
}
思路2:动态规划
dp[t][i] 表示t时间内到达城市i需要的最少通行费用总和。 dp[0][0] = passingFees[0];
注意:因为要对默认maxValue的取值 + passingFees 所以要防止溢出,取 int.MaxValue / 2
csharp
public class Solution{
public int MinCost(int maxTime, int[][] edges, int[] passingFees){
int n = passingFees.Length;
int[,] dp = new int[maxTime+1,n]; //dp[t,i]
int maxValue = int.MaxValue / 2;
for(int i=0; i<=maxTime; i++){
for(int j=0; j<n; j++){
dp[i,j] = maxValue;
}
}
dp[0,0] = passingFees[0];
for(int t=1; t<=maxTime; t++){
for(int index=0; index<edges.Length; index++){
int start = edges[index][0];
int end = edges[index][1];
int cost = edges[index][2];
if(cost <= t){
dp[t,start] = Math.Min(dp[t,start], dp[t-cost,end] + passingFees[start]);
dp[t,end] = Math.Min(dp[t,end], dp[t-cost,start] + passingFees[end]);
}
}
}
int result = maxValue;
for(int t=1; t<=maxTime; t++){
result = Math.Min(result,dp[t,n-1]);
}
return result == maxValue ? -1 : result;
}
}
复习: Bellman-Ford 算法
注意点:
- 初始化 passingFees 的时候,如果最后是返回 dp[maxTime,n-1] 则需要初始化任何时间到0的 passingFee
- 否则的话,最后就需要遍历dp数组,找到恰好某个时间到达终点的最小花费,参考上面代码,此时的话赋值 dp[0,0]=passingFee[0]即可
- 注意图是无向的,所以在 转移的时候,注意加入 fee 根据目的地不同加入不同的 fee,是 source 的还是 target 的
csharp
public class Solution {
public int MinCost(int maxTime, int[][] edges, int[] passingFees) {
//Bellman Ford 算法
int n = passingFees.Length;
int[,] dp = new int[maxTime+1,n]; //dp[t,j]表示t时间内,从0到j所需要的花费
//初始化
int INF = 0x3f3f3f3f;
for(int i=0; i<=maxTime; i++){
for(int j=0; j<n; j++){
dp[i,j] = INF;
}
}
for(int t=0; t<=maxTime; t++){
dp[t,0] = passingFees[0]; //从0到0,需要初始花费
}
for(int t=1; t<=maxTime; t++){
for(int j=0; j<edges.Length; j++){
int source = edges[j][0];
int target = edges[j][1];
int cost = edges[j][2];
if(t >= cost){
//双向的,所以可以从source-->target 也可以反向
dp[t,target] = Math.Min(dp[t,target], dp[t-cost,source] + passingFees[target]);
dp[t,source] = Math.Min(dp[t,source], dp[t-cost,target] + passingFees[source]);
}
}
}
return dp[maxTime,n-1] >= INF ? -1 : dp[maxTime,n-1];
}
}
 AlgoPress
AlgoPress