Appearance
1824. 最少侧跳次数
题目描述
https://leetcode.cn/problems/minimum-sideway-jumps/description/
给你一个长度为 n 的 3 跑道道路 ,它总共包含 n + 1 个 点 ,编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 ,它想要跳到点 n 处。然而道路上可能有一些障碍。
给你一个长度为 n + 1 的数组 obstacles ,其中 obstacles[i] (取值范围从 0 到 3)表示在点 i 处的 obstacles[i] 跑道上有一个障碍。如果 obstacles[i] == 0 ,那么点 i 处没有障碍。任何一个点的三条跑道中 最多有一个 障碍。
比方说,如果 obstacles[2] == 1 ,那么说明在点 2 处跑道 1 有障碍。
这只青蛙从点 i 跳到点 i + 1 且跑道不变的前提是点 i + 1 的同一跑道上没有障碍。为了躲避障碍,这只青蛙也可以在 同一个 点处 侧跳 到 另外一条 跑道(这两条跑道可以不相邻),但前提是跳过去的跑道该点处没有障碍。比方说,这只青蛙可以从点 3 处的跑道 3 跳到点 3 处的跑道 1 。 这只青蛙从点 0 处跑道 2 出发,并想到达点 n 处的 任一跑道 ,请你返回 最少侧跳次数 。
注意:点 0 处和点 n 处的任一跑道都不会有障碍。
示例 1: 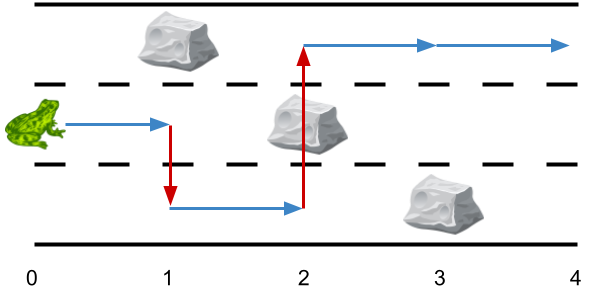
输入:obstacles = [0,1,2,3,0]
输出:2
解释:最优方案如上图箭头所示。总共有 2 次侧跳(红色箭头)。
注意,这只青蛙只有当侧跳时才可以跳过障碍(如上图点 2 处所示)。
示例 2: 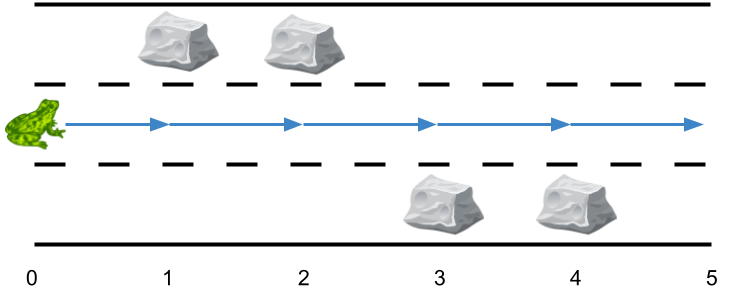
输入:obstacles = [0,1,1,3,3,0]
输出:0
解释:跑道 2 没有任何障碍,所以不需要任何侧跳。
示例 3:
输入:obstacles = [0,2,1,0,3,0]
输出:2
解释:最优方案如上图所示。总共有 2 次侧跳。
提示:
- obstacles.length == n + 1
- 1 <= n <= 5 * 10^5
- 0 <= obstacles[i] <= 3
- obstacles[0] == obstacles[n] == 0
思路:动态规划
定义一定要清楚,我们定义dp[i,j]表示当前i点的每一条道到达需要的最小侧跳次数。
所以,当 i,j 处有障碍时,是无法到达那个点的,我们把它设置为 INF 最大值 那么其他点,则可以由前面直接跳过来 dp[i,j] = dp[i-1,j] 或者有前面其他点+1步跳过来。 如果当前点的跑道被设置为 INF 了,那么也不能由前面的那个跑道跳过来。 如示例1中,在 i=2 处, 跑道1有障碍了,我们不能由前面的i=1的跑道1跳过来。 综上:计算方法是,先直接从前面跳过来,然后计算统计当前跑到是INF的,其他跑到的最小值+1,然后和当前跑到直接跳过来的步数相比较取小。
csharp
public class Solution {
public int MinSideJumps(int[] obstacles) {
//动态规划,下一个状态取决于上一个状态
//dp[i,1]表示到这一条道需要前面需要跳动几次
int n = obstacles.Length;
int INF = obstacles.Length+1;
int[,] dp = new int[n,4];
dp[0,1] = 1;
dp[0,2] = 0;
dp[0,3] = 1;
for(int i=1; i<n; i++){
//从前面直接过来,或者前面其他两个地方过来+1
int minCount = INF;
for(int j=1; j<=3; j++){
if(j == obstacles[i]){
dp[i,j] = INF;
}
else{
dp[i,j] = dp[i-1,j]; //从前面直接跳过来
minCount = Math.Min(minCount,dp[i-1,j]);//直接当前没障碍的地方才能统计最小值
}
}
//Console.WriteLine("minCount = {0}",minCount);
//看是否从直接调过来划算,还是从其他地方跳过来更划算
for(int j=1; j<=3; j++){
if(j != obstacles[i]){
dp[i,j] = Math.Min(dp[i,j], minCount+1);
}
}
}
// for(int i=0; i<n; i++){
// Console.WriteLine("{0},{1},{2}",dp[i,1],dp[i,2],dp[i,3]);
// }
return Math.Min(Math.Min(dp[n-1,1],dp[n-1,2]),dp[n-1,3]);
}
}
因为下一个状态之和上一个状态有关,我们可以使用滚动数组
csharp
public class Solution {
public int MinSideJumps(int[] obstacles) {
//动态规划,下一个状态取决于上一个状态
int n = obstacles.Length;
int INF = n + 1;
int[] dp = new int[4];
dp[1] = 1;
dp[3] = 1;
for(int i = 1; i < n ;i++){
int minCount = INF;
for(int j=1; j<=3; j++){
if(j == obstacles[i]){
dp[j] = INF;
}
else{
minCount = Math.Min(minCount,dp[j]);
}
}
for(int j=1;j<=3;j++){
if(j != obstacles[i]){
dp[j] = Math.Min(dp[j],minCount+1);
}
}
}
return Math.Min(dp[1],Math.Min(dp[2],dp[3]));
}
}
 AlgoPress
AlgoPress