AlgoPressAppearance
0119-杨辉三角II
https://leetcode.cn/problems/pascals-triangle-ii
给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。
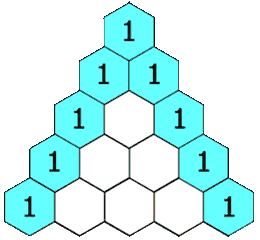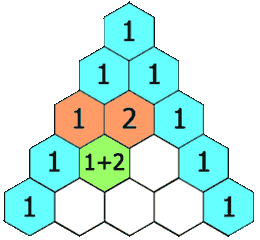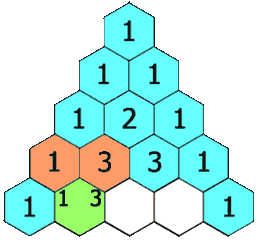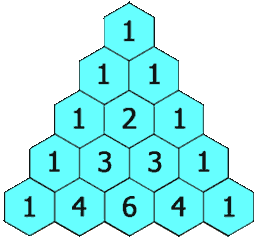
示例 1:
输入: rowIndex = 3
输出: [1,3,3,1]
示例 2:
输入: rowIndex = 0
输出: [1]
示例 3:
输入: rowIndex = 1
输出: [1,1]
提示:
0 <= rowIndex <= 33
进阶：
你可以优化你的算法到 O(rowIndex) 空间复杂度吗？
基本思路
参考 118 杨辉三角，只返回 curList
参考代码
0 : 1
1 : 1 1
2 : 1 2 1
3 : 1 3 3 1
4 : 1 4 6 4 1
5 : 1 5 10 10 5 1
注意：如果第二层循环从前往后计算，就会 result[j-1]+result[j] 就会出现重复计算，比如 1 2 1, 计算为 1 3 4 1第三个数计算的时候，前面的2，变成3了
但是如果倒着计算，就不会影响到前面的数的结果
csharp
public class Solution {
public IList<int> GetRow(int rowIndex) {
List<int> result = new List<int>();
result.Add(1);
for(int i=1; i<=rowIndex; i++){
for(int j=i; j>0;j--){
if(j==i){
result.Add(1);//最后一个
}
else{
int value = result[j-1]+result[j];
result[j] = value;
}
}
}
return result;
}
}
进阶思路:数学算法
TODO： 会溢出
csharp
public class Solution{
public IList<int> GetRow(int rowIndex){
List<int> result = new List<int>();
result.Add(1);
for(int i=1; i<=rowIndex; i++){
result.Add(result[i-1] * (rowIndex - i + 1)/i);
}
return result;
}
}