Appearance
0045-跳跃游戏II
https://leetcode.cn/problems/jump-game-ii
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示: $$ 1 <= nums.length <= 10^4 \ 0 <= nums[i] <= 1000 $$
思路分析
思路1 : 反向查找
因为题目给出了一定会到达最后位置
目标是到达数组最后一个位置,考虑最后一步跳跃前所在的位置,该位置通过跳跃能够到达最后一个位置。
如果有多个位置可以到达最后一个位置,那么【贪心】选择最远的那个(就是从最开始的循环,满足条件即可)
该方法可能会超时,最差情况下每个数都是1,每次都要从头循环一次
思路2 : 正向查找可达到的最大位置
实现代码
思路1:反向查找
csharp
class Solution{
public int Jump(int[] nums){
int position = nums.Length - 1;
int steps = 0;
while(position > 0){
for(int i=0; i<position; i++){
//从前往后查找,找到目标位置,就将结束坐标提前
if( i + nums[i] >= position){
position = i;
steps++;
break;
}
}
}
return steps;
}
}
思路2 : 正向查找可达到的最大位置
正向查找,每次找到可达到的最远位置,就可以得到最少的跳跃次数
比如,对于数组[2,3,1,2,4,2,3],初始下标是0,从下标0出发,最远可以达到2,下标0可到达位置中,下标1的值是3,从下标1可以出发最远可到达4, 从下标2出发,最远可达到下标3。 所以选择 max 4作为新的终点,steps + 1.
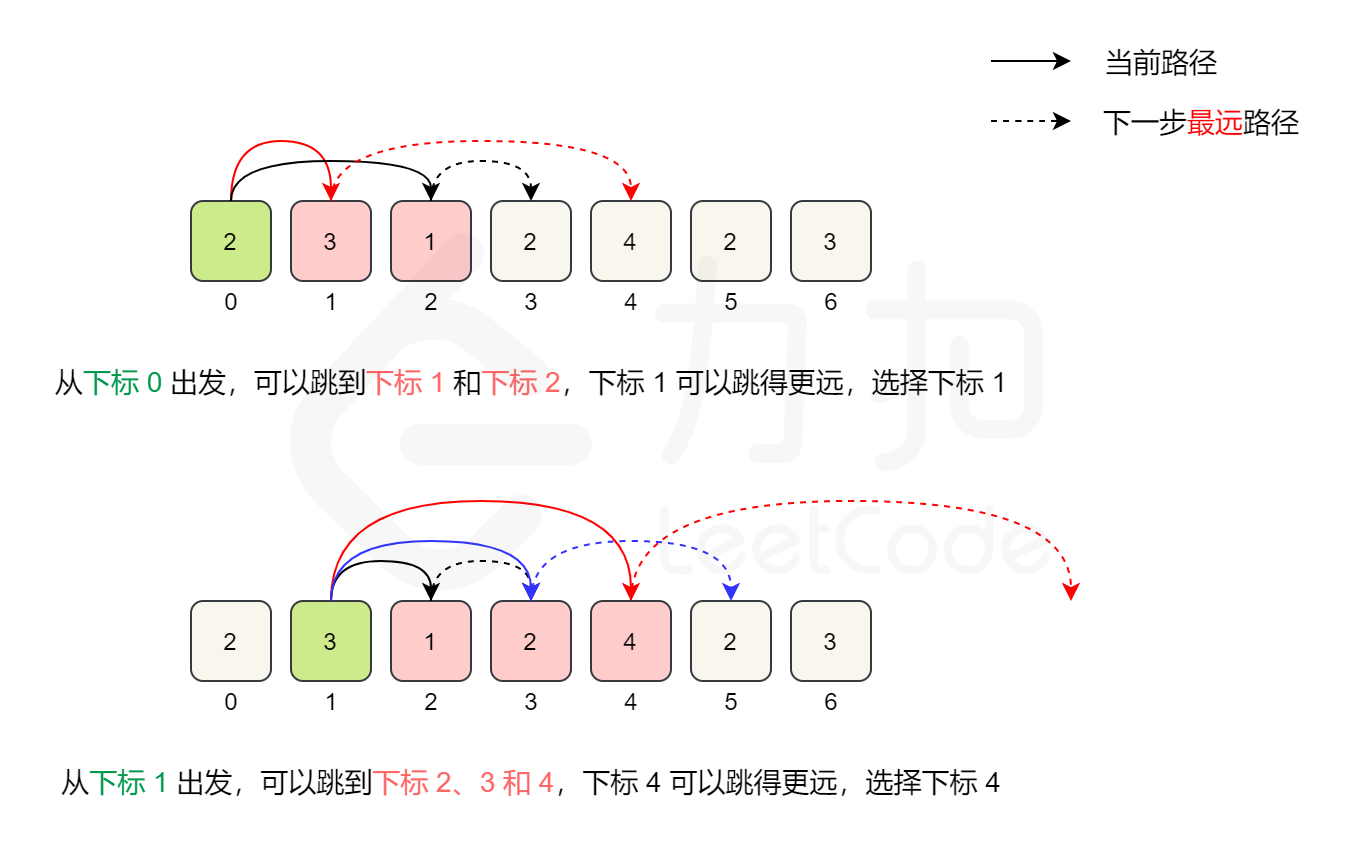
这个应该属于贪心算法
从第一步开始,首先跳出最大的距离, 将 reach 设置到该位置
继续遍历,处理 计算 nums[i]+i 能跳出的最大距离,记为 nextReach ,当 i = reach 的时候,正好前面一批遍历完。 因为后面要继续处理 steps++
这时看起来是从 reach 出开始跳的,实际上可以是从最大距离的那个 index 跳到 nextReach , 因为次数是一样的,所以可以直接处理。
因为肯定是会到最后一步的,所以循环到 < nums.Length - 1 即可,前面已经 steps ++ ,所以不需要计算最后一步需要跳动的次数
==思想就一句话:每次在上次能跳到的范围(end)内选择一个能跳的最远的位置(也就是能跳到nextReach位置的点)作为下次的起跳点 !==
csharp
class Solution{
public int Jump(int[] nums){
int reach = 0; //上次跳跃可达范围的右边界(下次的最右起跳点)
int steps = 0;
int nextReach = 0; //下次跳跃的最右点
//因为肯定会到达最后一位的,不用计算最后一次,否则会重复计算
//在同一个循环中,同时计算了下一次的max和移动当前的起跳点,很巧妙
for(int i=0; i<nums.Length - 1; i++){
nextReach = Math.Max(i+nums[i],nextReach);
if(i == reach){
reach = nextReach;
steps++;
}
}
return steps;
}
}
思路3: 动态规划
定义 dp 数组, dp[i] 表示到目前i为止需要的最小步数 初始化 dp[0] = 0, 因为 从0到0不需要跳跃 从 i=1, dp[i] 开始后,循环从前面 j : 0 ~ i-1 的位置,当 nums[i]+j 大于等于当前的下标,说明可以从 j 加一步跳过来 因为有多个可能,取最小值,所以初始化的时候,要 dp[i] = int.MaxValue 状态转移方程 dp[i] = Math.Min(dp[i],dp[j]+1)
csharp
class Solution{
public int Jump(int[] nums){
//定义 dp 表示到达目前为止的最小步数
int[] dp = new int[nums.Length];
dp[0] = 0;
for(int i=1; i<nums.Length; i++){
dp[i] = int.MaxValue;
for(int j=0; j<i; j++){
if(nums[j]+j>=i){
dp[i] = Math.Min(dp[i],dp[j]+1);
}
}
}
return dp[nums.Length-1];
}
}
复习:贪心
csharp
class Solution{
public int Jump(int[] nums){
int steps = 0;
int reach = 0;
int nextReach=0;
for(int i=0; i<nums.Length; i++){
nextReach = Math.Max(nextReach, i+nums[i]); //下一次可以达到的位置
if(i == reach || i == nums.Length-1){ //到达目标位置,或者到达结尾
steps++;
reach = nextReach;
}
}
return steps-1; //因为第1次 等于0 的时候也算了一步,所以总步数 -1
}
}
复习:20220622
csharp
public class Solution {
public int Jump(int[] nums) {
//从0出发,先计算能达到的最大距离
//这样到达这个距离的时候,必须跳一步,然后再步进过程中,找到下一跳的最大距离
//当i循环到 reach的时候,就增加步数
int reach = 0;
int nextReach = 0;
int count = 0;
for(int i=0; i<nums.Length; i++){
nextReach = Math.Max(nextReach,nums[i]+i); //下一跳能到达的最大距离
if(reach == i || i == nums.Length - 1){ //如果直接到末尾了,直接步数加1退出
count++;
reach = nextReach;
}
}
return count-1; //因为最后一步实际上是不需要跳的,所以总的结果减1
}
}
 AlgoPress
AlgoPress