Appearance
0041-缺失的第一个正数
https://leetcode.cn/problems/first-missing-positive
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
提示:
1 <= nums.length <= 5 * 105
-231 <= nums[i] <= 231 - 1
基本思路【官方】
题目说复杂度 O(n),但是可以循环多次的 O(常数*n) = O(n)
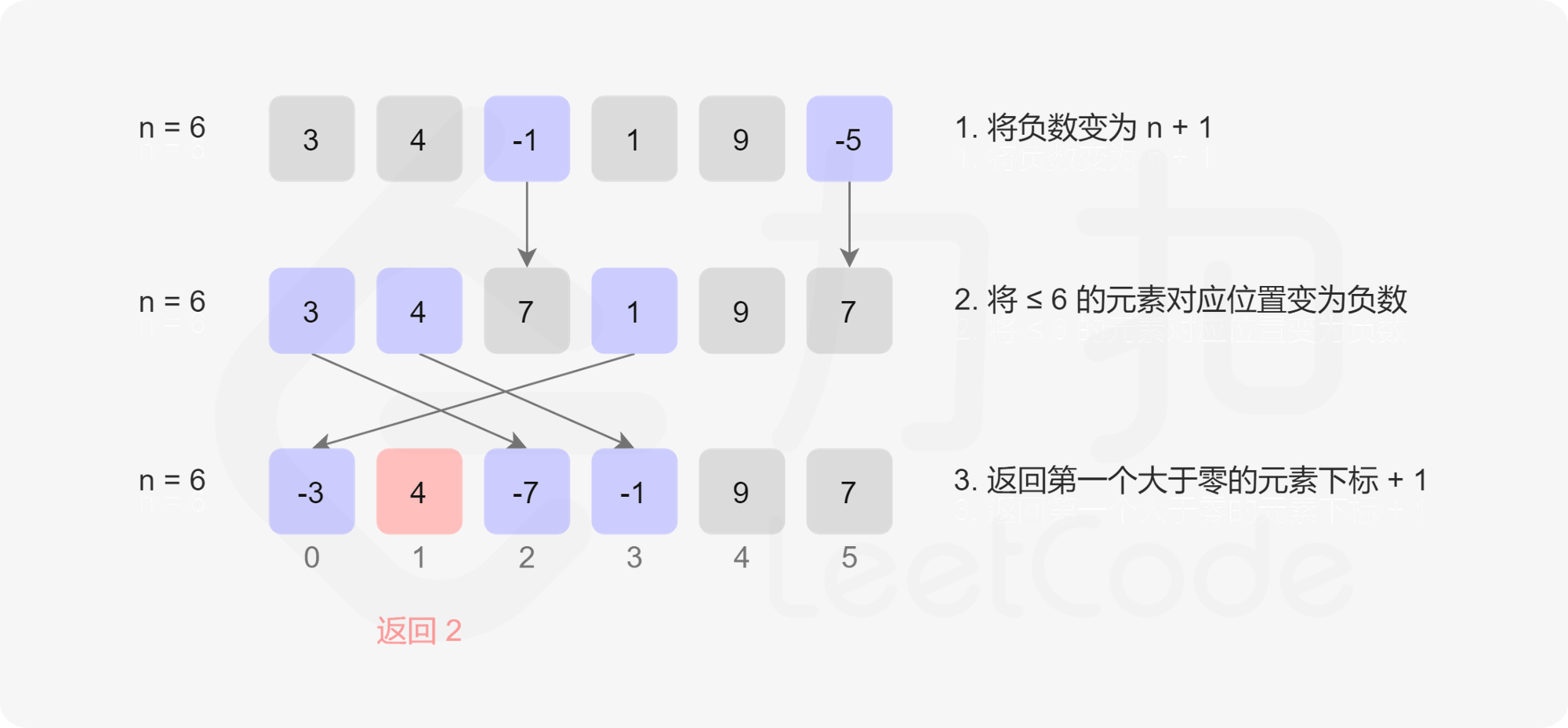
思路: 1~n个数当中,如果缺失的,那么他一定是位于 1~n 的,如果都存在,那么答案是 n+1
- 将负数都修改成 n+1 的值,排除在结果外面
- 将其他的小于n的数字打标记,打标记的方式为把目标的单元格的数字变成负数,超过 n 的可以不管 这里要注意:打完标记的数字会变成负数,所以我们要用 abs 取值来判断
- 遍历,找到没有变成负数的下标,说明没有该正整数,返回 i+1
- 如果都没有找到,则返回 n + 1
参考代码
csharp
public class Solution {
public int FirstMissingPositive(int[] nums) {
int n = nums.Length;
//处理负数
for(int i=0; i < n; i++){
if(nums[i] <= 0){
nums[i] = n + 1;
}
}
//打标记
for(int i=0; i < n; i++){
int num = Math.Abs(nums[i]); //因为目标数据可能先被更新为负数了,所以要使用abs取值, 测试用例 [3,4,-1,1]
if(num <= n ){
nums[num-1] = - Math.Abs(nums[num-1]); //用ABS防止重复计算, 比如两个数字4都指向了 i=3
}
}
//寻找没有打标记的下标
for(int i=0; i < n; i++){
if(nums[i] > 0){
return i+1;
}
}
//没找到,返回n+1
return n+1;
}
}
思路二【官方】
1~n个数字,如果没有缺少,那么可以正好排序号 0~n-1的位置中去。 所以我们将数组的数字交换到应该的位置去,如果都成功了,缺少的数字就是 n+1, 如果某处断开了,那么那个数字就是缺少的正整数
csharp
public class Solution {
public int FirstMissingPositive(int[] nums) {
int n = nums.Length;
for(int i=0; i<n; i++){
//while 循环持续交换
while(nums[i] > 0 && nums[i] <=n && nums[i] != nums[nums[i]-1]){
//swap
//Console.WriteLine("nums[i]={0}",nums[i]);
//注意交换的依赖关系 nums[i] = nums[nums[i]-1]
int temp = nums[i];
nums[i] = nums[temp-1];
nums[temp-1] = temp;
}
}
//循环看不是那个位置的数字
for(int i=0; i<n; i++){
if(nums[i] != i+1){
return i+1;
}
}
return n+1;
}
}
复习:20220703
注意 1. n 取 nums.Length 2. 设置 -Math.Abs(nums[num-1])
csharp
public class Solution {
public int FirstMissingPositive(int[] nums) {
int n = nums.Length;
//第一步,不在范围内的数字,都是设置为n+1
for(int i=0; i<n; i++){
if(nums[i] <= 0){
nums[i] = n + 1;
}
}
//第二步,更新坐标
for(int i=0; i<n; i++){
int num = Math.Abs(nums[i]); //次出用abs是因为数据可能已经被更新为负数了
if(num <= n ){
nums[num-1] = -Math.Abs(nums[num-1]);
}
}
//第三步,返回还是正数的
for(int i=0; i<n; i++){
if(nums[i] > 0){
return i+1;
}
}
return n+1;
}
}
 AlgoPress
AlgoPress